

When f=p, the right-hand-side acts as the representative of the pressure force. Here, the minus sign in the left-hand-side provides an explanation that the normal n⃗ n→ to S points inward, and ∇f happens to be the f’s gradient.
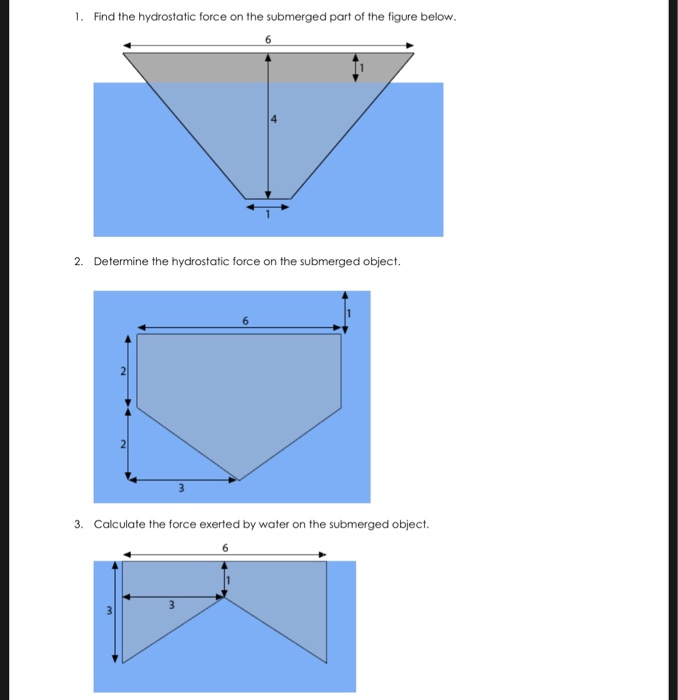
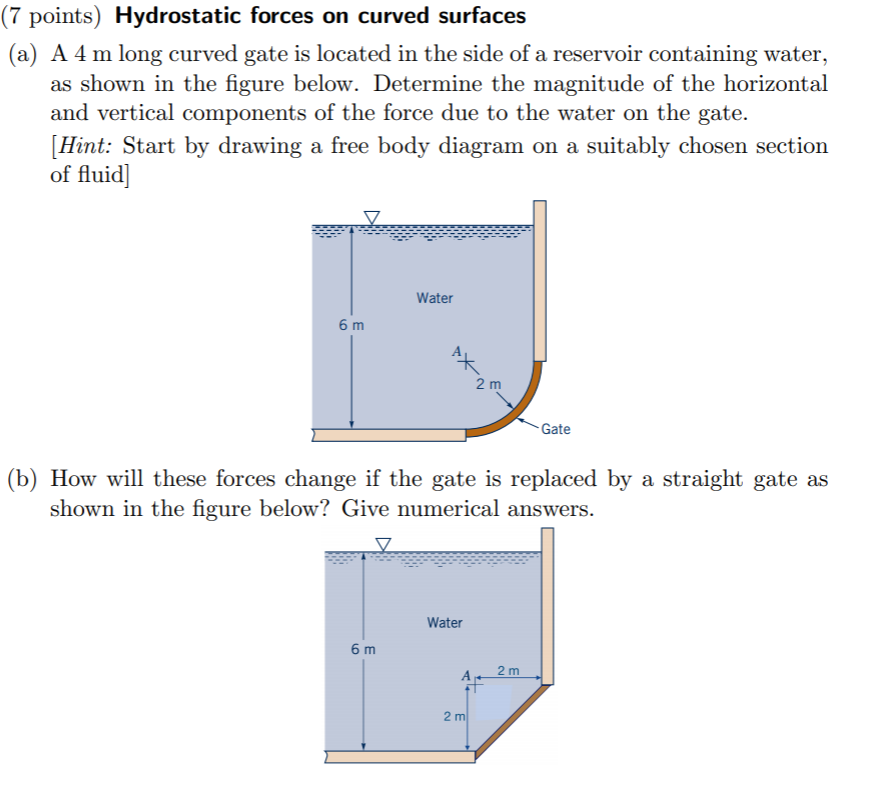
In practical situations, when fluid density turns out to be uniform in practical situations, Eq. (1) yieldsĪt this stage, p0 is nothing more than a constant of integration that is keyed to a choice of being a z-axis’ origin.įor any function of space (field) f that one can define in a closed volume V that is bounded by the surface S, Gauss’ divergence theorem give an explanation that The left-hand-side is an exact derivative because p is not dependent on the horizontal coordinates. Calling ρ as the local fluid density and g as the acceleration of gravity, a balance of vertical forces on a fluid element yields the well-known result: Here, the absolute pressure p is by definition hydrostatic, i.e., p=ph. Experts define an ( x, y, z) coordinate system where the vertical z-axis points upward. The consideration of a basic case of a stagnant fluid first takes place, where only weight and pressure forces are significant. Therefore, one must know these quantities so as to determine a particular liquid’s hydrostatic pressure. Furthermore, the main factors which influence it are the liquid’s density and the local gravity. The liquid’s hydrostatic properties are not constant. Furthermore, the height of a liquid column, of uniform density, is such that it turns out to be directly proportional to the hydrostatic pressure. Hydrostatic pressure refers to the pressure whose generation takes place by the weight of liquid above a measurement point when the liquid is in a state of rest. 2 FAQs on Hydrostatic Pressure Introduction to Hydrostatic Pressure


 0 kommentar(er)
0 kommentar(er)
